Calculating the Mean of a Data Set
The mean, or average, is a fundamental statistical measure that represents the center of a dataset by balancing values above and below it. It is widely used in fields like business, healthcare, and education. This section explains the mean, its formulas, and how to calculate it manually and with technology. Through examples, we will see how the mean helps summarize and interpret data efficiently.
Mean
What is the Mean?
The mean, also commonly known as the average, is the sum of all data values divided by the number of values. The sample mean is often denoted as \( \bar{{x}} \), while the population mean is denoted as \( \mu \). The mathematical formulas for calculating the mean are:
\[ \begin{align*} \textbf{Population Mean: }&& \mu &= \dfrac{\sum x}{{N}} \\\\ \textbf{Sample Mean: } &&\bar{{x}} &= \dfrac{\sum x}{{n}} \end{align*} \]What do these symbols mean?
Although the primary focus of this text is interpretation, it is still a math textbook, so we will encounter mathematical symbols and formulas throughout. To aid our understanding, we will explain these symbols as they appear, especially since many of these will be used repeatedly throughout this text.
- The symbol \( \sum \) means "sum" or "add everything up."
- The symbol \( x \) represents individual data values.
- \( N \) denotes the total number of values in a population and is often referred to as the population size.
- \( n \) denotes the number of values in a sample and is often referred to as the sample size.
It is important to note that \( \sum \) cannot stand alone; it must be followed by another symbol specifying what is being summed. In our formulas, we see \( \sum x \) in the numerator, which instructs us to "add up all the data values." This notation is especially useful when dealing with large datasets containing hundreds or thousands of values, as it eliminates the need to list each number individually.
Why do we have two formulas for mean?
Populations and samples each have their own formulas for related concepts, such as the mean. In this case, the formulas are functionally identical, but as we explore other topics later in this chapter, we will see that some formulas differ between populations and samples.
Additionally, note that \( \mu \) represents the population mean and is classified as a parameter, while \( \overline{{x}} \) represents the sample mean and is classified as a statistic.
But why do we use \( \mu \) (pronounced "mew" and written in English as "mu") instead of a more familiar letter? By convention, parameters (which describe populations) are often represented by Greek letters, whereas statistics (which describe samples) are typically denoted using more familiar Latin letters from the English alphabet.
Now that we know the formulas for mean and how to interpret them, let's do a quick example to make sure we understand how to perform a calculation.
Example
Consider the following data representing test scores of five students on their first exam: 75, 80, 85, 90, 95. Use this data to calculate the average exam score for this sample.
| Score |
|---|
| 75 |
| 80 |
| 85 |
| 90 |
| 95 |
Solution
To find the mean of this sample, sum all the test scores and divide by the number of scores. In mathematical terms, we calculate: \[ \sum x = 75 + 80 + 85 + 90 + 95 = 425 \] since \( x \) represents an individual test score and \( \sum x \) means to sum all the test scores. The sample size is 5, so we have \( n = 5 \). Combining this information, the final calculation is: \[ \begin{align*} \bar{{x}} &= \dfrac{\sum x}{{n}} \ &= \dfrac{75 + 80 + 85 + 90 + 95}{{5}} \ &= \dfrac{{425}}{{5}} \ &= 85 \end{align*} \] $$\tag*{\(\blacksquare\)}$$
Now that we understand how to calculate the mean, let's focus on what this number actually represents. One way to think about the mean is in terms of wealth redistribution. In society, some people have more money than others. The mean, or average, represents the amount each person would have if we could redistribute wealth so that everyone had exactly the same amount.
We can see this concept clearly using our previous example. Notice that the score of 75 is 10 points below the mean, while the score of 95 is 10 points above the mean. If we take 10 points from the person who scored 95 and give them to the person who scored 75, both students would now have 85 points. Similarly, since the score of 80 is 5 points below the mean and the score of 90 is 5 points above the mean, we can transfer 5 points from the student who scored 90 to the student who scored 80, so that both also end up with 85. After these adjustments, every student has a score of 85.
This illustrates what the mean represents—it balances out values above and below average to give a single number that evenly distributes the data across all individuals in the sample or population.
Of course, we don’t actually redistribute scores or money in this way. The purpose of the mean is to help us understand the central tendency of a dataset—the balance point between those with the highest values and those with the lowest.
Our next example provides an interactive way to illustrate this concept of balancing.
Example 2
Complete the Understanding the Idea of Average Value/Mean interactive example below.
Now that we understand what a mean is and how to calculate a mean, we need to see how to calculate the mean using a technology since many datasets number in the hundreds and thousands. Manually calculating large datasets is time-consuming and prone to errors; in these circumstances, it is okay to let the technology do the heavy lifting.
Example
The following Law School Admission Test (LSAT) scores for a sample of 50 students are given below. Find the mean of the sample using the Summary Statistics Calculator.
| LSAT Scores | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 174 | 172 | 169 | 176 | 169 | 170 | 175 | 171 | 168 | 177 |
| 165 | 180 | 173 | 166 | 178 | 170 | 174 | 167 | 179 | 172 |
| 163 | 181 | 171 | 164 | 177 | 169 | 175 | 168 | 180 | 170 |
| 162 | 182 | 170 | 165 | 176 | 168 | 174 | 166 | 178 | 171 |
| 161 | 183 | 169 | 167 | 175 | 167 | 173 | 165 | 177 | 172 |
Solution
We load the data into the Summary Statistics Calculator with its default settings, and \(\overline{{x}}\) is calculated automatically. The result is \(\overline{{x}}\approx 171.68\).
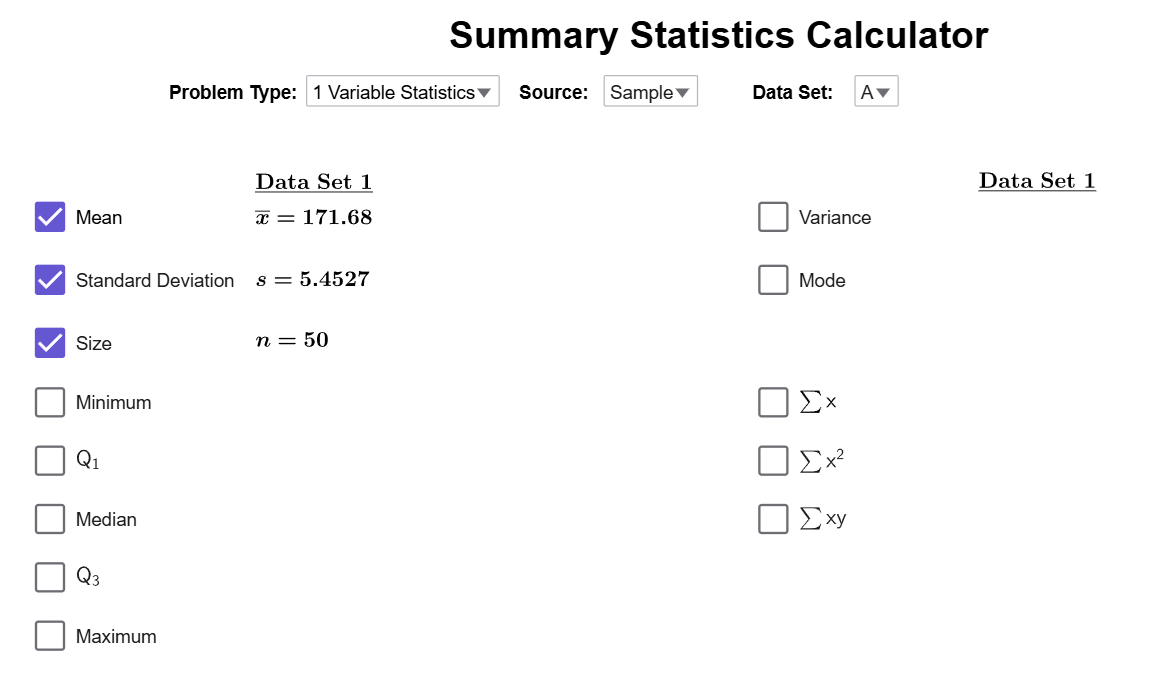
$$\tag*{\(\blacksquare\)}$$
Conclusion
The mean provides a simple yet powerful way to understand the central tendency of a dataset. It balances values above and below it, making it a key tool for data analysis. While calculating the mean manually is useful for small datasets, technology is essential for handling larger ones efficiently. Understanding the mean is a crucial step in mastering statistical analysis as we will be repeatedly using the mean throughout this entire text.